栈总结

原理

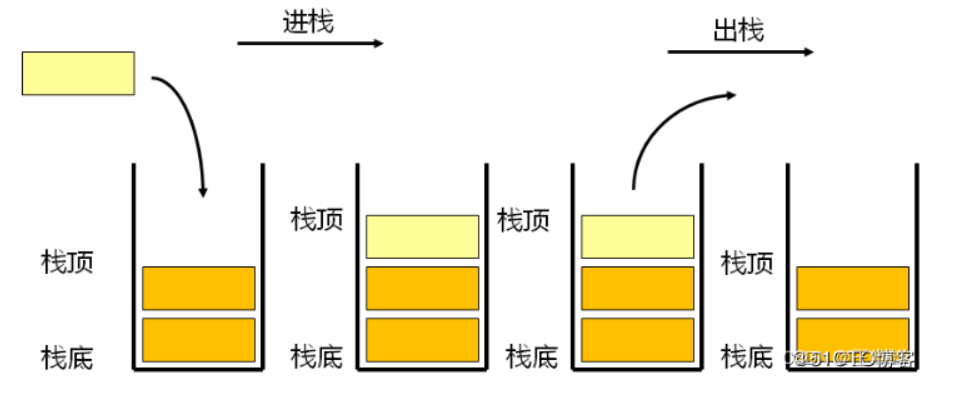
栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

常见的实现

通过数组实现

通过index指针来实现对元素的访问

优点：

实现简单
内存存储连续
随机访问

缺点：
容量固定，而且难以修改

struct Stack{ //Stack with array
    int data[100];
    int index;
    Stack(){
        index=-1;
    }
    void push(int x){
        index++;
        data[index]=x;
    }
    int top(){
        return data[index];
    }
    int pop(){
        int temp=data[index];
        index--;
        return temp;
    }
    bool isEmpty(){
        if(index==-1){
            return true;
        }
        return false;
    }
};

通过链表实现

用链表替代数组的作用，通过index指针来实现对元素的访问
优点：

容量不限制
更加灵活

缺点：

实现复杂
内存空间不连续

struct Node{
    int data;
    Node *next;
    Node(int x){
        data=x;
        next=nullptr;
    }
};
struct LinkedStack{
    Node *head;
    int Size;
    LinkedStack(){
        this->head=new Node(-1);
        Size=0;
    }
    void push(int x){
        Node *temp=new Node(x);
        temp->next=head->next;
        head->next=temp;
        Size++;
    }
    int pop(){
        Node *temp=this->head->next;
        int d=temp->data;
        this->head->next=temp->next;
        delete temp;
        Size--;
        return d;
    }
    int top(){
        return this->head->next->data;
    }
    bool isEmpty(){
        if(this->Size==0){
            return true;
        }
        return false;
    }
    int GetSize(){
        return this->Size;
    }

};

常见的应用

括号匹配检查

利用栈结构，扫描字符串，遇到左括号就压栈，遇到右括号就退栈

int main(){
    LinkedStack s;
    string str;
    cin>>str;
    for(int i=0;i<str.length();i++){
        if(str[i]=='['){
            s.push(str[i]);
        }else if(str[i]==']'){
            char temp=s.pop();
            if(temp!='['){
                goto NOT;
            }

        }else if(str[i]=='('){
            s.push(str[i]);
        }else if(str[i]==')'){
            char temp=s.pop();
            if(temp!='('){
                goto NOT;
            }
        }else if(str[i]=='{'){
            s.push(str[i]);
        }else if(str[i]=='}'){
            char temp=s.pop();
            if(temp!='{'){
                goto NOT;
            }
        }else{
            continue;
        }
    }
    if(s.isEmpty()==true){
        cout<<"match!!!"<<endl;
    }else{
        NOT:cout<<"not match"<<endl;
    }

    return 0;
}

中缀表达式转后缀表达式


int main(){
    m['+']=0;//四则运算优先级
    m['-']=0;
    m['*']=1;
    m['/']=1;
    LinkedStack s;
    cout<<"输入一个中缀表达式:";
    string str;cin>>str;
    cout<<"后缀表达式为:";
    for(int i=0;i<str.length();i++){
        if(str[i]==' '){
            continue;
        }
        if(str[i]<='9'&&str[i]>='0'){
            cout<<str[i];
        }
        else if(str[i]=='('){
            s.push(str[i]);
        }
        else if(str[i]==')'){
            //直到遇到左括号
            while(!s.isEmpty()){
                if(s.top()=='('){
                    s.pop();
                    break;
                }
                cout<<s.pop();
            }
        }
        else if(str[i]=='+'||str[i]=='-'||str[i]=='*'||str[i]=='/'){
            while(!s.isEmpty()&&m[str[i]]<=m[s.top()]&&s.top()!='('){
               cout<<s.pop();
            }
            s.push(str[i]);
        }
    }
    while(!s.isEmpty()){ //打印剩余
        cout<<s.pop();
    }
    cout<<endl;
    return 0;
}

后缀表达式计算

int main(){
    LinkedStack s;
    string str;cin>>str;
    for(int i=0;i<str.length();i++){
        if(str[i]==' '){
            continue;
        }
        if(str[i]<='9' && str[i]>='0'){
            s.push(str[i]-'0');
        }else if(str[i]=='+'){
            int a=s.pop();
            int b=s.pop();
            s.push(a+b);
        }
        else if(str[i]=='-'){
            int a=s.pop();
            int b=s.pop();
            s.push(b-a);
        }
        else if(str[i]=='*'){
            int a=s.pop();
            int b=s.pop();
            s.push(a*b);
        }
        else if(str[i]=='/'){
            int a=s.pop();
            int b=s.pop();
            s.push(b/a);
        }
    }
    int result=s.pop();
    cout<<"result is "<<result<<endl;
    return 0;
}

原理