原理
树是一种数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个节点有零个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树。
树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
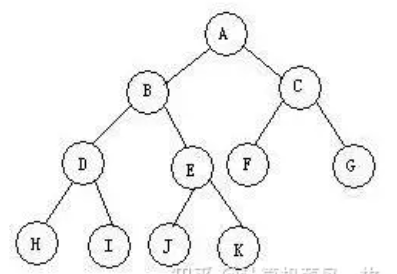
相关概念
祖先节点: 根到结点的唯一路径上的所有结点
兄弟节点: 有相同双亲的结点
结点的度: 树中一个结点的孩子个数
树的度: 树中结点的最大度数
结点的深度: 从根结点开始自顶向下逐层累加的。
结点的高度: 从叶结点开始自底向上逐层累加的。
树的高度(或深度): 树中结点的最大层数。
有序树和无序树: 树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。假设图为有序树,若将子结点位置互换,则变成一棵不同的树。
森林: m (m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这m棵树作为该结点的子树,则森林就变成了树。
二叉树
特点
- 二叉树每个结点的度最多为2
- 结点的子树有左右之分,不能随意调换,调换后又是一棵新的二叉树。
三种特殊形态
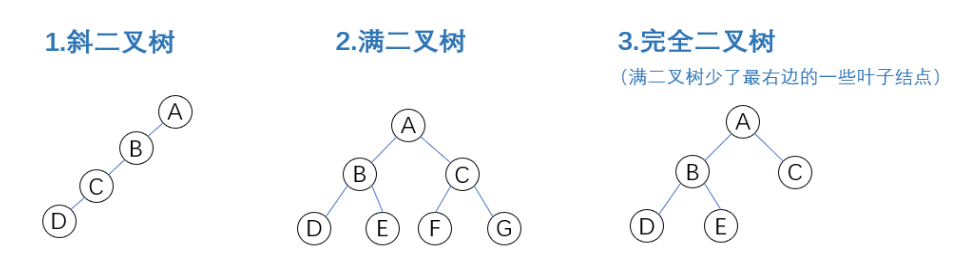
相关计算
NULL
完全二叉树最少的节点个数是2^(h - 1),最多的节点个数是2^n-1(此时是满二叉树状态)
树的存储
二叉树:孩子兄弟表示法
struct TNode{
T data;
TNode* left; //左子树
TNode* right; //右子树
}树的创建
层序创建
需要借助队列
struct TNode{
int data;
TNode* left;
TNode* right;
};
class Tree{
private:
TNode* root;
public:
Tree(){
queue<TNode*> q;
int data_temp;
TNode *node;
cin>>data_temp;
if(data_temp!=0){
root=new TNode;
root->data=data_temp;
root->left=nullptr;
root->right=nullptr;
q.push(this->root);
}
else{
this->root=nullptr;
return;
}
while(!q.empty()){
node=q.front();q.pop();
cin>>data_temp;
if(data_temp==0){
node->left=nullptr;
}else{
TNode* node_temp=new TNode;
node_temp->data=data_temp;
node_temp->left=nullptr;
node_temp->right=nullptr;
node->left=node_temp;
q.push(node_temp);
}
cin>>data_temp;
if(data_temp==0){
node->right=nullptr;
}else{
TNode* node_temp=new TNode;
node_temp->data=data_temp;
node_temp->left=nullptr;
node_temp->right=nullptr;
node->right=node_temp;
q.push(node_temp);
}
}
cout<<"Tree has been created!"<<endl;
}
};遍历方法
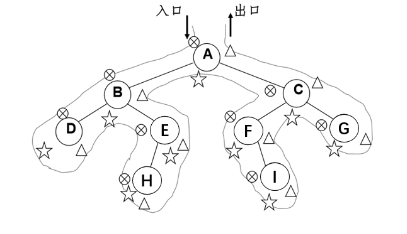
X序遍历指的是根节点的位置
中序遍历:左-中-右
前序遍历:中-左-右
后序遍历:左-右-中
中序遍历
递归实现
实现简单,效率较低
void InorderTravel(TNode* t){
if(t!=nullptr){
this->PreTravel(t->left);
cout<<t->data<<" ";
this->PreTravel(t->right);
}
}非递归实现
实现稍复杂,效率稍高
需要借助栈
void InorderTravelWithoutRecursion(){
TNode* t=this->root;
stack<TNode*> s;
while(t!=nullptr||!s.empty()){
while(t!=nullptr){
s.push(t);
t=t->left;
}
t=s.top();s.pop();
cout<<t->data<<" ";
t=t->right;
}
cout<<endl;
}前序遍历
递归实现
void PreTravel(TNode* t){
if(t!=nullptr){
cout<<t->data<<" ";
this->PreTravel(t->left);
this->PreTravel(t->right);
}
}后序遍历
递归实现
void PostTravel(TNode* t){
if(t!=nullptr){
this->PreTravel(t->left);
this->PreTravel(t->right);
cout<<t->data<<" ";
}
}层序遍历
非递归实现
需要借助队列
void LevelOrderTravel(){
queue<TNode*> q;
TNode* node=this->root;
if(node==nullptr){return;}
q.push(node);
while(!q.empty()){
node=q.front();q.pop();
cout<<node->data<<" ";
if(node->left!=nullptr){
q.push(node->left);
}
if(node->right!=nullptr){
q.push(node->right);
}
}
cout<<endl;
}相关操作
获取所有的叶子节点
void GetLeaves(TNode* t){
if(t!=nullptr){
if((t->left==nullptr && t->right==nullptr)){
cout<<t->data<<" ";
}else{
this->GetLeaves(t->left);
this->GetLeaves(t->right);
}
}else{
return;
}
}获取树的高度
int GetHeight(TNode* t){
if(t!=nullptr){
int leftH=this->GetHeight(t->left);
int rightH=this->GetHeight(t->right);
return max(leftH,rightH)+1;
}
}