树总结（二）——搜索二叉树

特点

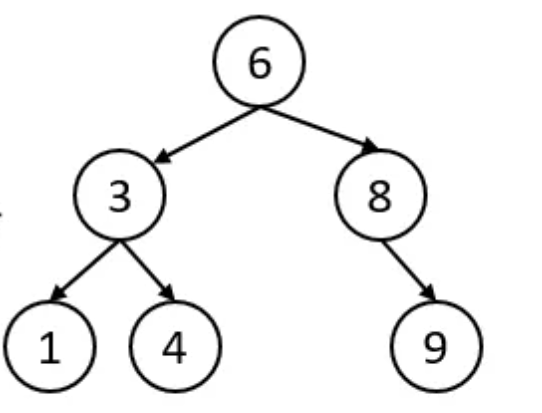
二叉搜索树（Binary Search Tree）也叫二叉查找树，他是具有下列性质的一种二叉树。

• 若左子树不空，则左子树上所有节点的值都小于根节点的值；

• 若右子树不空，则右子树上所有节点的值都大于根节点的值；

• 任意节点的子树也都是二叉搜索树；

• 中序遍历结果一定是有序的，而且是从小到大排序的

相关操作

这里的二叉树采用链式存储，函数采用递归函数的方式。

搜索二叉树的定义

struct Node{ //定义一个节点
    int data; //数据区域
    Node* left; //左子树
    Node* right; //右子树
};
class BST{
private:
    Node* root; //数据区域

    Node* Insert(Node* T,int x);
    void InOrder(Node* T);
    Node* Find(Node* T,int x);
    Node* FindMin(Node* T);
    Node* FindMax(Node* T);
public:
    BST(){
        this->root=nullptr;
    }
    void insert(int x); //插入数据
    int min(); //获得最小元
    int max(); //获得最大元
    Node* find(int x);  //递归搜索
    Node* findA(int x); //非递归搜索
}

方法实现

插入

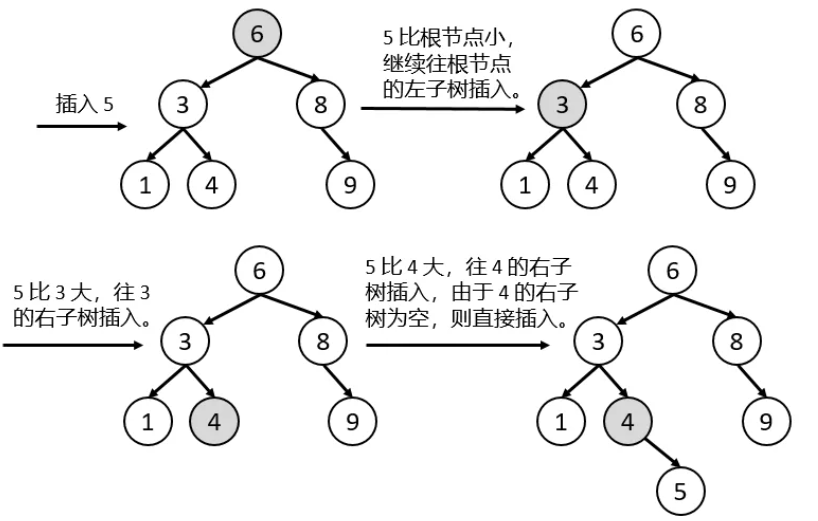
Node* BST::Insert(Node* T,int x){
    if(T==nullptr){
        T=new Node;
        T->data=x;
        T->left=nullptr;
        T->right=nullptr;
        if(this->root==nullptr){
            this->root=T;
        }
    }else{
        if(x<T->data){
            T->left=this->Insert(T->left,x);
        }else if(x>T->data){
            T->right=this->Insert(T->right,x);
        }
    }
    return T;
}

void BST::insert(int x){
    this->Insert(this->root,x);
}

搜索

通常情况下来说，非递归的实现相比于递归的实现来说效率要更高一些

递归的实现

Node* BST::findA(int x){
    Node* T=this->root;
    while(T!=nullptr){
        if(x>T->data){
            T=T->right;
        }else if(x<T->data){
            T=T->left;
        }else{
            break;
        }
    }
    return T;
}

递归实现

Node* BST::Find(Node* T,int x){
    if(T==nullptr){
        return nullptr;
    }else if(T->data<x){
        return T->right;
    }else if(T->data>x){
        return T->left;
    }else{
        return T;
    }
}

Node* BST::find(int x){
    return this->Find(this->root,x);
}

获取最大元

找右子树找到底

Node* BST::FindMin(Node* T){
    if(T==nullptr){
        return nullptr;
    }
    else if(T->left==nullptr){
        return T;
    }else{
        return this->FindMin(T->left);
    }
}

int BST::max(){
    return this->FindMax(this->root)->data;
}

获取最小元

找左子树找到底

Node* BST::FindMin(Node* T){
    if(T==nullptr){
        return nullptr;
    }
    else if(T->left==nullptr){
        return T;
    }else{
        return this->FindMin(T->left);
    }
}

int BST::min(){
    return this->FindMin(this->root)->data;
}