树总结（四）——应用

大/小根堆（优先队列）

原理

最大（小）堆是指在树中，存在一个结点而且该结点有儿子结点，该结点的data域值都大于等于其儿子结点的data域值，并且它是一个完全二叉树。根结点都表示树中的最小元素结点。最大堆的根结点是树中元素最大的。实为二叉树的一种

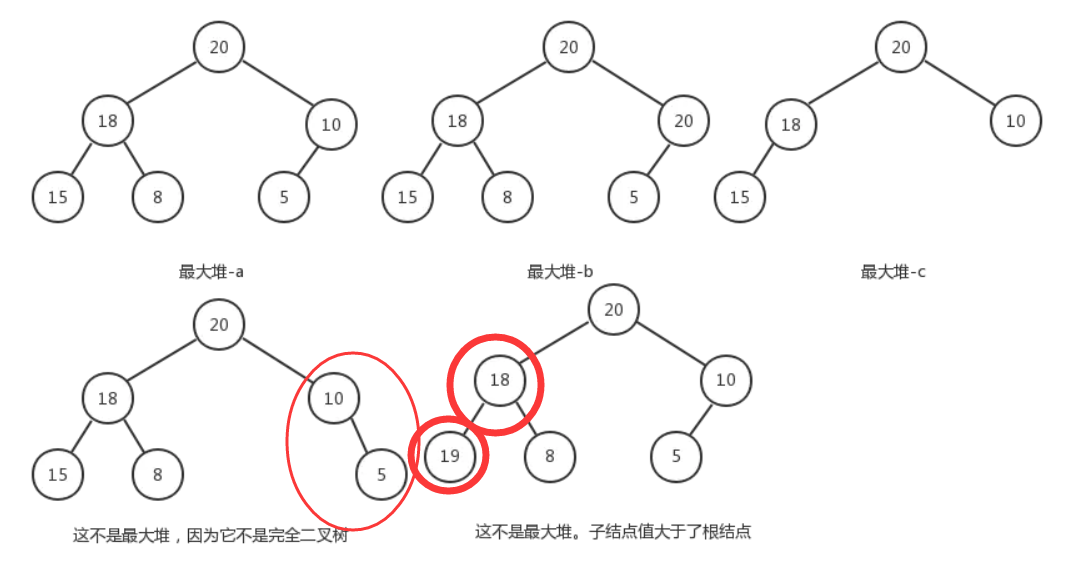
特点

• 最大堆的根结点是树中元素最大的
• 最小堆的根结点是树中元素最小的
• 兄弟节点之间没有严格的约束关系，可以是左>右，也可以左<右

实现

采用数组的方式存储

以下以大根堆为例子，小根堆同理。

定义

class MaxHeap{
private:
    int cap;
    int size;
    int* data;

public:
    MaxHeap(int MaxSize){
        this->cap=MaxSize;
        this->size=0;
        this->data=new int[MaxSize+1];
    }
    bool empty()
    bool full();
    bool push(int x);
    int pop();
    int top();
};

判断是否为空

bool MaxHeap::empty(){
    if(this->size==0){
        return true;
    }
    return false;
}

判断是否为满

bool MaxHeap::full(){
    if(this->cap==this->size){
        return true;
    }
    return false;
}

插入

bool MaxHeap::push(int x){
    if(this->full()){
        return false;
    }
    this->size++;
    for(int i=this->size;this->data[i/2]<x;i/=2){ //拿x的值和节点作比较，当x比节点值大的时候，不断把指针上升
        this->data[i]=this->data[i/2];// 上滤x
    }
    this->data[i]=x;
    return true;
}

获取堆顶元素

int MaxHeap::top(){
    if(this->empty()){
        return -1;
    }
    return this->data[1];
}

弹出堆顶元素

int MaxHeap::pop(){
    if(this->empty()){
        return -1;
    }
    int parent,child;
    int max_item,x;
    max_item=this->data[1];
    x=this->data[this->size--];
    for(parent=1;parent*2<this->size;parent=child){
        child=parent*2;
        if((child!=this->size)&&(this->data[child]<this->data[child+1])){
            child++;
        }
        if(x>=this->data[child]){
            break;
        }else{
            this->data[parent]=this->data[child];
        }
    }
    this->data[parent]=x;
    return max_item;
}