图总结（一）——图的定义

图的定义

图有顶点和边组成，顶点用有穷非空集合V(G)={v1,v2,…,vn}表示，顶点之间的边用集合E(G)={(u,v)|u∈V,v∈V}表示，图可以表示为：G=(V,E)。其中G表示图，V表示顶点，E表示边。|V|表示顶点的个数，也称图的阶，|E|表示边的条数。

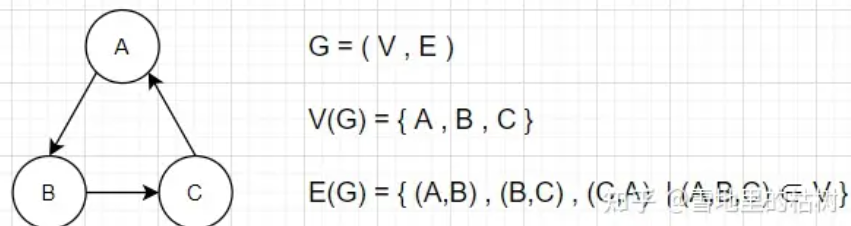
图的存储和创建

图可以通过邻接矩阵和邻接表的方式存储

邻接矩阵

原理

边使用二维数组存储，E[V][V]。横轴表示第一个顶点索引，纵轴表示第二个顶点索引，权值存储在二维数组的对于坐标位置。

无向图

有向图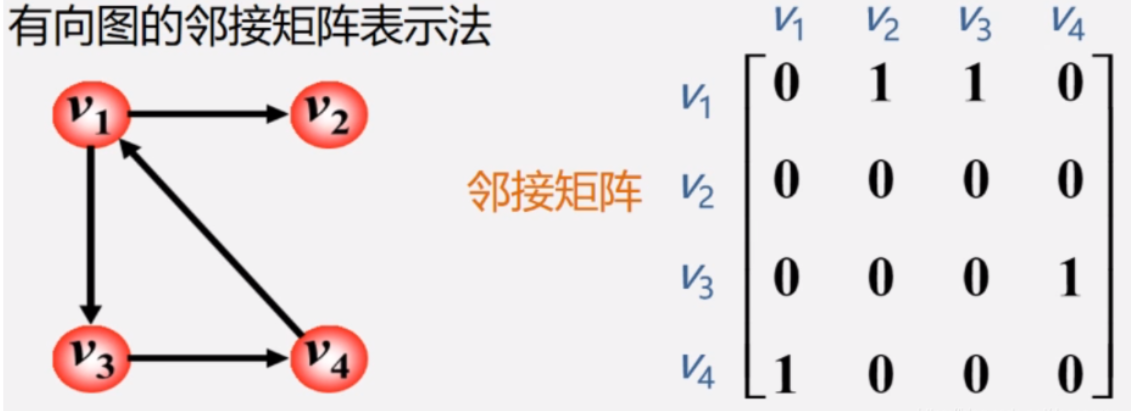

代码实现

#define INF 0x3f3f3f3f
struct ENode{
    int v1;
    int v2;
    int  weight;
};
class BasicGraph{
private:
    int Nv;
    int Ne;
    int G[500][500];
    char data[500];
    void create(int vertexNum){
        this->Nv=vertexNum;
        this->Ne=0;
        for(int i=0;i<vertexNum;i++){
            for(int j=0;j<vertexNum;j++){
                this->G[i][j]=INF;
            }
        }
    }
public:
    BasicGraph(){
        int Nvs;cout<<"输入点的个数:";cin>>Nvs;
        this->create(Nvs);
        cout<<"输入"<<Nvs<<"个顶点的数据:";
        for(int i=0;i<Nvs;i++){
            cin>>this->data[i];
        }
        cout<<"输入边的个数:";cin>>this->Ne;
        if(this->Ne!=0){
            ENode* e=new ENode;
            for(int i=0;i<this->Ne;i++){
                cout<<"输入第"<<(i+1)<<"条边的起点 终点 权重";
                cin>>e->v1>>e->v2>>e->weight;
                this->insert(e);
            }
        }
    }
    void insert(ENode* edge){
        this->G[edge->v1][edge->v2]=edge->weight;
        this->G[edge->v2][edge->v1]=edge->weight;
    }
};

邻接表

原理

使用链表存储顶点与边的关系，表头存储顶点索引，然后指下一条相连边，下一条相连边存储当前顶点与该边的相连顶点索引和权值，并指向下一条相连边，以此内推。

简言之：点用数组存储，每个点的first后是与该点邻接的点所组成的链表，插入采用头插法。

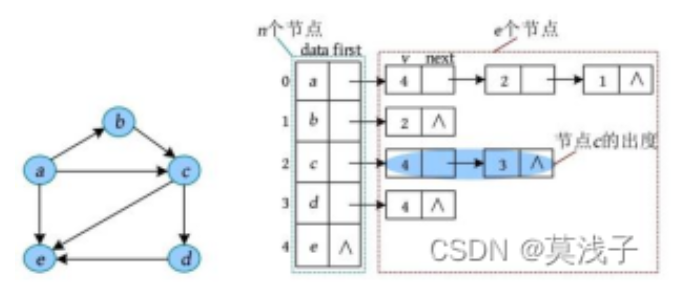
代码实现

struct ENode{   //边
    int v1;
    int v2;
    int weight;
};
struct AdjVNode{    //邻接表
    int adjV;       //邻接点的下标
    int weight;     //边的权重
    AdjVNode* next; //相接的下一个点
};
struct VertexNode{  //顶点
    char data;      //点的数据
    AdjVNode* first;    //邻接的第一个点
};
class LinkedGraph{
private:
    int Nv;
    int Ne;
    VertexNode G[500];
    void create(int vertexNum){
        this->Nv=vertexNum;
        this->Ne=0;
        for(int i=0;i<vertexNum;i++){
            this->G[i].first=nullptr;
        }
    }
public:
    LinkedGraph(){
        int Nvs;cout<<"输入点的个数:";cin>>Nvs;
        this->create(Nvs);
        cout<<"输入"<<Nvs<<"个顶点的数据:";
        for(int i=0;i<Nvs;i++){
            cin>>(this->G[i].data);
        }
        cout<<"输入边的个数:";cin>>this->Ne;
        if(this->Ne!=0){
            ENode* e=new ENode;
            for(int i=0;i<this->Ne;i++){
                cout<<"输入第"<<(i+1)<<"条边的起点 终点 权重";
                cin>>e->v1>>e->v2>>e->weight;
                this->insert(e);
            }
        }
    }
    void insert(ENode* e){
        AdjVNode* node=new AdjVNode;
        node->adjV=e->v2;
        node->weight=e->weight;
        node->next=this->G[e->v1].first;
        this->G[e->v1].first=node;
        //无向图
        AdjVNode* node1=new AdjVNode;
        node1->adjV=e->v1;
        node1->weight=e->weight;
        node1->next=this->G[e->v2].first;
        this->G[e->v2].first=node1;
    }
};